1/4 Of A Circle Graph

The get-go matter you need to know in order to graph the equation of a circle is where on a plane the heart is located. The equation of a circle appears as

This is called the middle-radius form (or standard form) because it gives you both pieces of information at the same time. The h and v stand for the center of the circle at point (h, 5), and r names the radius. Specifically, h represents the horizontal displacement — how far to the left or to the right the heart of the circle falls from the y-axis. The variable 5 represents the vertical displacement — how far above or below the center falls from the 10-axis.

You tin count from the center r units (the radius) horizontally in both directions and vertically in both directions. This will give y'all four different points, all equidistant from the center. Connect these iv points with the best curve that you can sketch to get the graph of the circumvolve.

Center at the origin

The simplest circle to graph has its centre at the origin (0, 0). Because both h and v are zero, they tin disappear and y'all can simplify the standard circle equation to look like

For case, to graph the circumvolve

follow these steps:

Realize that the circumvolve is centered at the origin (no h and five) and place this indicate there.
Calculate the radius by solving for r.

Set r-squared = sixteen. In this case, you go r = iv.
Plot the radius points on the coordinate plane.

You count out 4 in every direction from the center (0, 0): left, right, up, and downwards.
Connect the dots to graph the circumvolve using a smooth, circular bend.

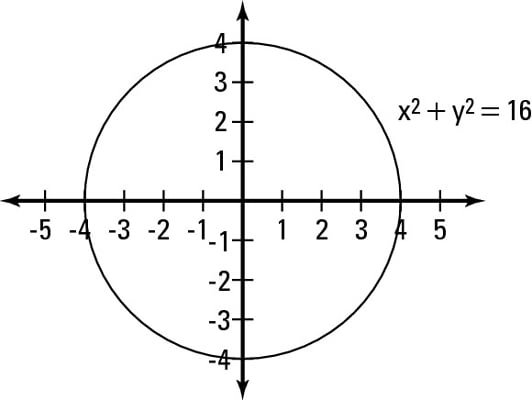
This figure shows this circle on the plane.

Center abroad from the origin

Graphing a circle anywhere on the coordinate plane is pretty easy when its equation appears in eye-radius form. All you practice is plot the middle of the circle at (h, k), and then count out from the eye r units in the four directions (upwards, down, left, right). So, connect those four points with a nice, round circle.

Unfortunately, while it is much easier to graph circles at the origin, very few are every bit straightforward and simple as those. In pre-calc, you work with transforming graphs of all different shapes and sizes (this is nothing new to you, right?). Fortunately, these graphs all follow the aforementioned pattern for horizontal and vertical shifts, so y'all don't have to remember many rules.

Don't forget to switch the sign of the h and five from inside the parentheses in the equation. This is necessary considering the h and v are inside the grouping symbols, which means that the shift happens contrary from what you would think.

For case, to graph the equation

Locate the heart of the circle from the equation (h, v).

Place the center of the circumvolve at (3, –ane).
Calculate the radius past solving for r.
Plot the radius points on the coordinate plane.

Count 5 units upward, down, left, and right from the center at (iii, –i). This ways that you lot should take points at (8, –i), (–two, –1), (3, –vi), and (iii, 4).
Connect the dots to the graph of the circle with a round, smooth curve.

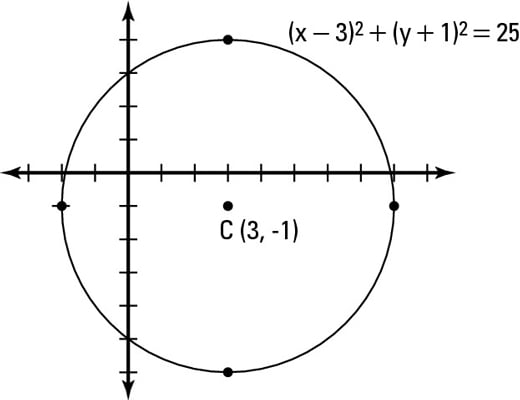
This effigy gives you a visual representation of this circle.